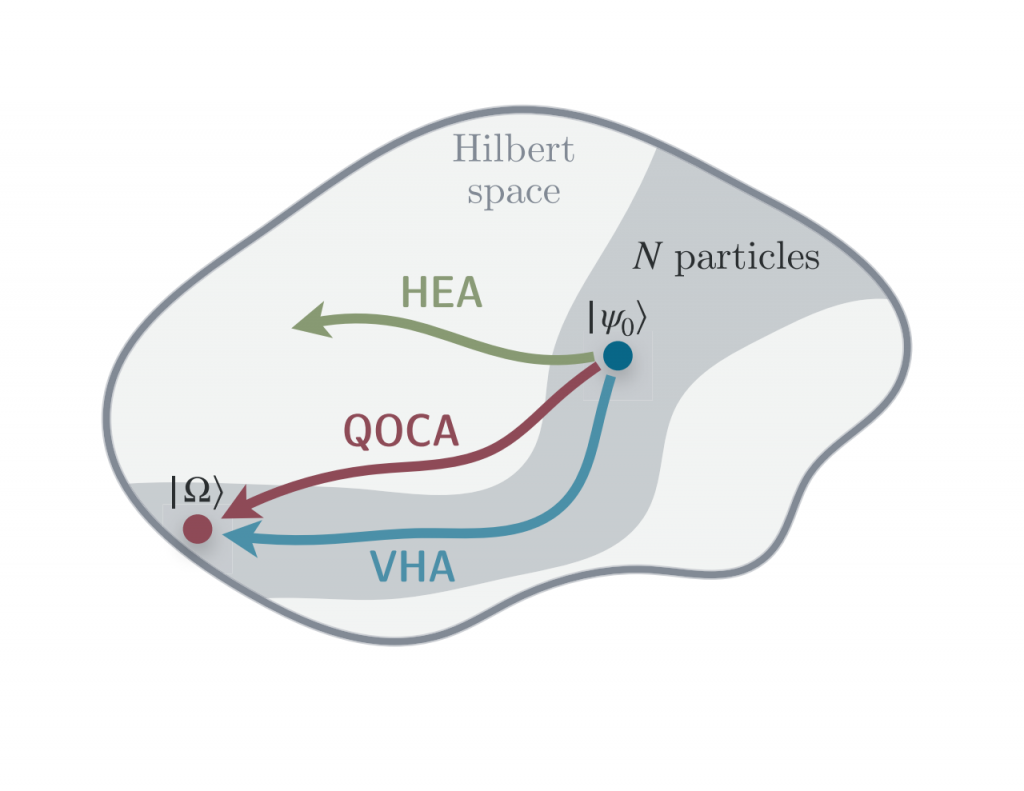
Un élément central des algorithmes quantiques variationnels (AQV) est le circuit de préparation de l’état, également appelé ansatz ou forme variationnelle. Ce circuit est le plus souvent conçu de manière à exploiter les symétries de l’Hamiltonien du problème et, de cette façon, à limiter la recherche variationnelle à un sous-espace d’intérêt. Ici, nous montrons que cette approche n’est pas toujours avantageuse en introduisant des ansatzes qui incorporent des unitaires brisant les symétries. Cette classe d’ansatz, que nous appelons ansates inspirées du contrôle optimal quantique (QOCA), est inspirée de la théorie du contrôle optimal quantique et conduit à une meilleure convergence des VQAs pour certains problèmes importants. En effet, nous comparons QOCA à des formes variationnelles populaires appliquées au modèle de Fermi-Hubbard à demi-remplissage et montrons que nos circuits variationnels peuvent approcher l’état fondamental de ce modèle avec une grande précision. Nous montrons également comment QOCA peut être utilisé pour trouver l’état fondamental de la molécule d’eau et comparons les performances de notre ansatz par rapport à d’autres choix courants utilisés pour les problèmes de chimie. Ce travail constitue un premier pas vers le développement d’une classe plus générale d’ansatz brisant la symétrie avec des applications aux problèmes de physique et de chimie.
https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.3.023092
